Cómo clasificar algoritmos con Big O Notation

En esta serie de artículos, cubrimos la importancia del análisis de la complejidad de los algoritmos, la implementación de la búsqueda binaria, la clasificación a través de MergeSort y QuickSort. Siempre mencionamos la Big O Notation de una manera muy abstracta e intuitiva. ¿Qué tal si ahora los estudiamos mas a profundidad?

INTRODUCCIÓN

En nuestro contexto tecnológico actual, con las más diversas máquinas y potencias de procesamiento y almacenamiento volátil, sería inviable medir algoritmos solo contando el tiempo que se ejecutan. Entonces, ¿cómo podemos saber que un algoritmo funciona mejor que el otro?

Como cubrimos en los artículos mencionados anteriormente, una gran opción es calcular aproximadamente la cantidad de operaciones que realiza el algoritmo. Pero, ¿cuáles son estas operaciones?

Caso mejor, peor y promedio

Para explicarlo mejor, recordemos la primera solución de búsqueda de estudiantes en la que usamos la búsqueda lineal. Decidimos que revisaríamos a todos los estudiantes de la lista hasta que encontráramos lo que buscábamos. Así que vamos a pensar en algunas posibilidades?

Supongamos que tenemos la lista de estudiantes en orden alfabético y estamos buscando al estudiante Brendo.

¡Mira que bueno! Lo encontramos en la primera posición de la lista y no necesitamos revisarlo más. Así que este será nuestro mejor caso.

Ahora tenemos que ir en busca del estudiante Nico.

Vimos que tomó la mitad de la lista para encontrarlo, así que supongamos que este es nuestro caso promedio.

¿Ahora vamos a encontrar al estudiante Wanessa?

Notamos que revisamos a todos los estudiantes hasta que lo encontramos, por lo que debemos considerar que este es el peor de los casos, ¿verdad? ¿Y dónde encaja Big O en esta historia? ¡Exactamente aquí! Big O es una notación que siempre tiene en cuenta el peor de los casos.

Pero, ¿por qué dividimos nuestra solución en tres casos si solo vamos a usar el peor? ¡Guarda esta información ya que pronto será muy importante!

Continuando, profundicemos en el análisis del peor de los casos: en él siempre tendremos que pasar por todos los alumnos. Qué significa eso?

Por cada estudiante agregado a nuestra lista, el algoritmo realizará una comparación más. ¿Entendemos esto mejor a través de un gráfico?

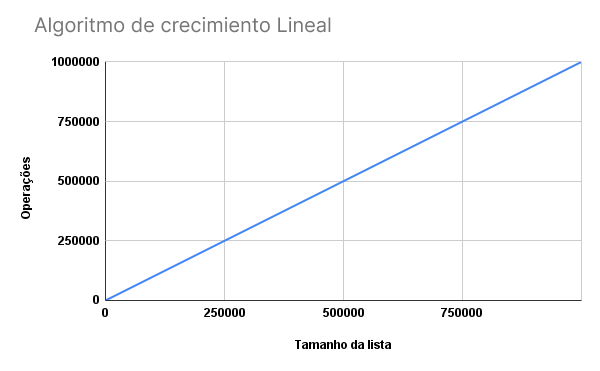
Ahora está claro que a medida que crece la lista, nuestro algoritmo crece linealmente en términos de sus operaciones. Entonces podemos considerarlo, en la Big O Notation, como O(N).

Es hora de ver nuestra segunda solución de búsqueda, la búsqueda binaria.

En esta solución también debemos considerar que hay una lista ordenada y con cada comparación en el medio de la lista, podemos descartar la mitad de la lista en la que no está el elemento.

Entonces nos damos cuenta de que el rendimiento será mucho mejor en comparación con la búsqueda lineal, ya que incluso en los peores casos no recorreremos todos los elementos.

Pero, ¿cuánto mejor es este algoritmo? ¡Veamos! Para comenzar nuestro análisis, revisemos nuestro mejor caso, que ocurre cuando buscamos el elemento en el medio de la lista.

Entonces podemos verificar que en el mejor de los casos, como en la búsqueda lineal, el binario también se comporta como O(1).

¿Y cuál sería el peor de los casos? ¿Cómo podemos calcular cuántas operaciones realizará nuestra búsqueda binaria? De forma muy intuitiva y teniendo en cuenta lo ya informado sobre el algoritmo, vamos a responder a estas dos preguntas.

Sabiendo que con cada comparación podemos descartar la mitad de la lista, pudimos inferir que la división de la lista por 2 sucesivamente nos traerá el número de operaciones realizadas con el conteo de las divisiones realizadas.

Aplicando el concepto de la lista anterior, que contenía 7 estudiantes, vemos que en el peor de los casos solo realizamos 3 comparaciones.

Ahora supongamos que tenemos 100 estudiantes, entonces en el peor de los casos haremos 7 comparaciones.

Notamos la gran diferencia entre las 100 comparaciones que realizamos en el peor de los casos de la búsqueda lineal con las 7 comparaciones que realizamos con la búsqueda binaria. !Veamos esto gráficamente!

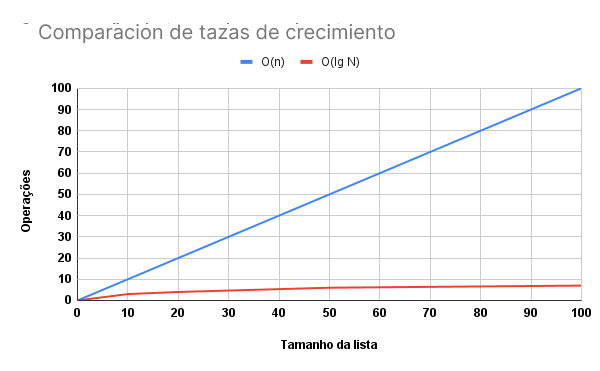
Y esta diferencia se hace aún más visible cuando aumentamos considerablemente el tamaño de la lista.

Pero, ¿es el algoritmo lineal el peor rendimiento que tenemos en tiempo de ejecución? Ya puedo decirte que no lo es, y podemos probarlo con el algoritmo de ordenación SelectionSort que explicamos en el artículo de implementación de la merge sort.

Hemos demostrado que tiene la notación asintótica de O(N²), así que veamos cuánto peor es gráficamente este algoritmo.

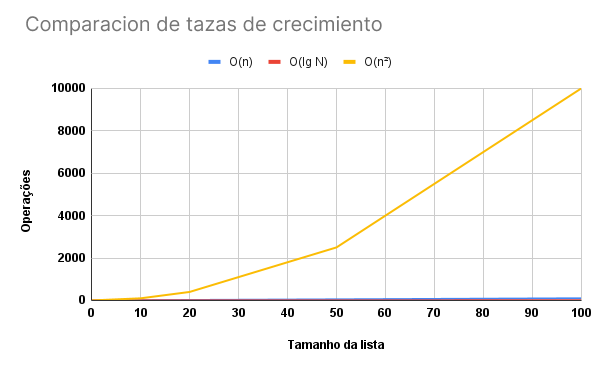
Vemos que nuestro algoritmo O(N²) cuadrático evoluciona exponencialmente en comparación con nuestros otros algoritmos que crecen discretamente en el gráfico. Y créanme, todavía hay algoritmos peores en eficiencia como O(n³), O(2ⁿ) pero que son temas para otras oportunidades.

Y con todo esto, se hace más evidente la importancia de conocer estos conceptos a la hora de implementar nuestros programas y nuestras funcionalidades.

Si ha seguido el rastro de artículos sobre complejidad de algoritmos, debe haber recordado una pregunta relacionada con la clasificación de algoritmos (Merge y Quick Sort): ¿Cómo elegir el mejor, entre algoritmos con la misma complejidad?

A continuación, explicaremos con más detalle qué factores y parámetros debemos evaluar en algoritmos con la misma complejidad en el siguiente artículo de la serie.

Brendo Rodrigo Souza de Matos

Ingeniero de Software apasionado por lo que hace, amante de los nuevos retos y sediento de conocimiento. Actualmente soy Ingeniero de Software de Plataformas en Méliuz (B3: CASH3) y estoy realizando una Maestría en Ciencias de la Computación en la Universidad Federal de Amazonas.

Este articulo fue adecuado para Alura Latam por: Wilfredo Rojas